Dental Arch of Children in Normal Occlusion

Introduction

The Primary dentition in children needs to be as close as possible to the ideal in order that during future adulthood, children may exhibit normal dental features like normal mastication and appearance, dental space and occlusion for proper and healthy functioning of permanent dentition. It is well known that physical appearances do directly impact on the self-esteem and inter-personal behaviour of the human individual, while dental health challenges like malocclusions, dental caries, gum disease and tooth loss do require preventive and curative interventions right from childhood so that permanent dentition may be normal in later years. The various parts of the dental arch during childhood, viz., canine, incisor and molar, play a vital role in shaping space and occlusion characteristics during permanent dentition [Prabhakaran et al., 2006]. Prabhakaran et al. even stress the importance of the arch dimensions in properly aligning teeth, stabilizing the form, alleviating arch crowding, and providing for a normal overbite and over jet, stable occlusion and a balanced facial profile. Thus, both research aims and clinical diagnosis and treatment have long required the study of dental arch forms, shape, size and other parameters like over jet and overbite, as also the spacing in deciduous dentition. In fact, arch size has been seen to be more important than even teeth size [Facal-Garcia et al., 2001]. While various efforts have been made to formulate a mathematical model for the dental arch in humans, the earliest description of the same has been by using terms like elliptic, parabolic, etc. Also, in terms of measurement, the arch circumference, width and depth have been identified by many experts as some of the relevant parameters for measuring the dental arch curve. In fact, some experts have even defined the dental arch curvature through use of biometry by measurement of ratios, angles and linear distances [Brader. 1972; Harris, 1997; Ferrario et al., 1997, 1999, 2001; Braun et al., 1998; Burris and Harris, 2000; Noroozi et al., 2001]. Such analysis, however, has serious limitations in describing a three-dimensional (3D) structure like the dental arch [Poggio et al.., 2000]. Thus, there are numerous mathematical models and geometrical forms that have been put forth by various experts, but no two models appear to be clearly defined by means of a single parameter [Noroozi et al., 2001]. This paper attempts to highlight, on the basis of a secondary research on available literature, the various mathematical approaches to defining the curvature of the dental arch of children in normal occlusion. It presents the assumptions, circumstances and limitations of each study, as well as an overall picture of the current stage of research in the field. It also arrives at the conclusion that further research, particularly by using modern imaging techniques and computer simulation could well provide for a better mathematical model for defining the dental arch of children in normal occlusion.

Defining the Dental Arch

Models for describing the dental arch curvature include conic sections [Biggerstaff, 1972; Sampson, 1981], parabolas [Jones and Richmond, 1989], cubic spline curves [BeGole, 1980], catenary curves [Battagel, 1996], and polynomials of second to eight degree [Pepe, 1975], mixed models and the beta function [Braun et al., 1998]. The definitions differ as because of differences in objectives, dissimilarity of samples studied and diverse methodologies adopted and uniform results in defining and arriving at a generalized model factoring in all symmetries and asymmetries of curvature elude experts even today. Some model may be suitable in one case while others may be more so in another situation. In this respect, conic sections which are 2^nd order curves, can only be applied to specific shapes like hyperbolas, eclipse, etc and their efficiency as ideal fit to any shape of the dental arch is thus limited [AlHarbi et al., 2006]. The beta function, although superior, considers only the parameters of molar width and arch depth and does not factor in other dental landmarks. Nor does it consider asymmetrical forms. In contrast, the 4^th order polynomial functions are better effective in defining the dental arch than either cubic spline or the beta function [AlHarbi et al., 2006]. AlHarbi and others [2006] also maintain that important considerations in defining the human dental arch through mathematical modelling like symmetry or asymmetry, objective, landmarks used and required level of accuracy do influence the actual choice of model.

Occlusion and its Types

Occlusion is the manner in which the lower and upper teeth intercuspate between each other in all mandibular positions or movements. Ash & Ramfjord [1982] state that it is a result of neuromuscular control of the components of the mastication systems viz., teeth, maxilla & mandibular, periodontal structures, temporomandibular joints and their related muscles and ligaments. Ross [1970] also differentiated between physiological and pathological occlusion, in which the various components function smoothly and without any pain, and also remain in good health. Furthermore, occlusion is a phenomenon that has been generally classified by experts into three types, namely, normal occlusion, ideal occlusion and malocclusion.

Ideal Occlusion

Ideal occlusion is a hypothetical state, an ideal situation. McDonald & Ireland [1998] defined ideal occlusions as a condition when maxilla and mandible have their skeletal bases of correct size relative to one another, and the teeth are in correct relationship in the three spatial planes at rest. Houston et al. [1992] have also given various other concepts relating to ideal occlusion in permanent dentition and these concern ideal mesiodistal & buccolingual inclinations, correct approximal relationships of teeth, exact overlapping of upper and lower arch both laterally and anteriorly, existence of mandible in position of centric relation, and also presence of correct functional relationship during mandibular excursions.

Normal Occlusion and its Characteristics

Normal occlusion was first clearly defined by Angle [1899] which was the occlusion when upper and lower molars were in relationship such that the mesiobuccal cusp of upper molar occluded in buccal cavity of lower molar and teeth were all arranged in a smoothly curving line. Houston et al., [1992] defined normal occlusion as an occlusion within accepted definition of the ideal and which caused no functional or aesthetic problems. Andrews [1972] had previously also mentioned about six distinct characteristics observed consistently in orthodontic patients having normal occlusion, viz., molar relationship, correct crown angulation & inclination, absence of undesirable teeth rotations, tightness of proximal points, and flat occlusal plane (the curve of Spee having no more than a slight arch and the deepest curve being 1.5 mm). To this, Roth [1981] added some more characteristics as being features of normal occlusion, viz., coincidence of centric occlusion and relationship, exclusion of posterior teeth during protrusion, inclusion of canine teeth solely during lateral excursions of the mandible and prevalence of even bilateral contacts in buccal segments during centric excursion of teeth. On the basis of a more recent research study, Oltramari et al. [2007] maintain that success of orthodontic treatments can be achieved when all static & functional objectives of occlusion exist and achieving stable centric relation with all teeth in Maxim intercuspal position is the main criteria for a functional occlusion

Mathematical Models for Measuring the Dental Arch Curve

Whether for detecting future orthodontic problems, or for ensuring normal occlusion, a study of the dental arch characteristics becomes essential. Additionally, intra-arch spacing also needs to be studied so as to help the dentist forecast and prevent ectopic or premature teeth eruption. While studies in the past on dentition in children and young adults have shown significant variations among diverse populations [Prabhakaran et al., 2006], dentists are continuously seized of the need to generalize their research findings and arrive at a uniform mathematical model for defining the human dental arch and assessing the generalizations, if any, in the dental shape, size, spacing and other characteristics. Prabhakaran et al. [2006] also maintain that such mathematical modelling and analysis during primary dentition is very important in assessing the arch dimensions and spacing as also for helping ensure a proper alignment in permanent dentition during the crucial period which follows the complete eruption of primary dentition in children. They are also of the view that proper prediction of arch variations and state of occlusion during this period can be crucial for establishing ideal desired esthetic and functional occlusion in later years.

While all dentists and orthodontists seem to be more or less unanimous in perceiving as important the mathematical analysis of the dental arch of children in normal occlusion, no two experts seem agreeable in defining the human dental arch by means of a single generalized model. A single model eludes the foremost dental practitioners owing to the differences in samples studied with regard to their origins, size, features, ages, etc. Thus while one author may have studied and derived his results from studying a sample of Brazilian children under some previously defined test conditions, another author may have studied Afro-American children of another age group, sample size or geographical origins. Also, within the same set of samples studied, there are also marked variations in dental arch shapes, sizes and spacing as found out by leading experts in the field. Shapes are also unpredictable as to the symmetry or asymmetry and this is another obstacle to the theoretical generalization that could evolve a single uniform mathematical model. However, some notable studies in the past decades do stand out and may be singled out as the most relevant and significant developments in the field till date.

The earliest models were necessarily qualitative, rather than quantitative. Dentists talked of ellipse, parabola, conic section, etc when describing the human dental arch. Earlier authors like Hayashi [1962] and Lu [1966] did attempt to explain mathematically the human dental arch in terms of polynomial equations of different orders. However, their theory could not explain asymmetrical features or predict fully all forms of the arch. Later on, authors like Pepe [1975], Biggerstaff [1972], Jones & Richmond [1989], Hayashi [1976], BeGole [1980], etc., made their valuable contributions to the literature in the dental field through their pioneering studies on teeth of various sample populations of children in general, and a mathematical analysis of the dental arch in particular. While authors like Pepe and Biggerstaff relied on symmetrical features of dental curvature, BeGole was a pioneer in the field in that he utilized the asymmetrical cubic splines to describe the dental arch. His model assumed that the arch could not be symmetrical and he tried to evolve a mathematical best fit for defining and assessing the arch curve by using the cubic splines. BeGole developed a FORTRAN program on the computer that he used for interpolating different cubic splines for each subject studied and essentially tried to substantiate a radical view of many experts that the arch curve defied geometrical definition and that such perfect geometrical shapes like the parabola or the ellipse could not satisfactorily define the same. He was of the view that the cubic spline appropriately represented the general maxillary arch form of persons in normal occlusion. His work directly contrasted efforts by Biggerstaff [1972] who defined the dental arch form through a set of quadratic equations and Pepe who used polynomial equations of degree less than eight to fit on the dental arch curve [1975]. In Pepe’s view, there could be supposed to exist, at least in theory, a unique polynomial equation having degree (n + 1) or less (n was number of data points) that would ensure exact data fit of points on the dental arch curve. An example would be the polynomial equation based on Le-Grange’s interpolation formula viz., Y = ⁿ_i=1y_i [j*i] (x-x_j)/x_i-x_j), where x_i, y_i were data points.

In 1989, Jones & Richmond used the parabolic curve to explain the form of the dental arch quite effectively. Their effort did contribute to both pre and post treatment benefits based on research on the dental arch. However, Battagel [1996] used the catenary curves as a fit for the arch curvature and published the findings in the popular British Journal of Orthodontics, proving that the British researchers were not far behind their American counterparts. Then, Harris [1997] made a longitudinal study on the arch form while the next year [1998], Braun and others put forth their famous beta function model for defining the dental arch. Braun expressed the beta function by means of a mathematical equation thus:

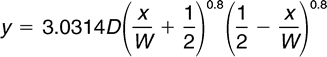
In the Braun equation, W was molar width in mm and denoted the measured distance between right and left 2^nd molar distobuccal cusp points and D the depth of the arch. A notable thing was that the beta function was a symmetrical function and did not explain observed variations in form and shape in actual human samples studied by others. Although it was observed by Pepe [1975] that 4^th order polynomials were actually a better fit than the splines, in later analyses in the 1990s, it appeared that these were even better than the beta [AlHarbi et al., 2006]. In the latter part of the 1990s, Ferrario et al. [1999] expressed the dental curve as a 3-D structure. These experts conducted some diverse studies on the dental arch in getting to know the 3-D inclinations of the dental axes, assessing arch curves of both adolescents and adults and statistically analysing the Monson’s sphere in healthy human permanent dentition. Other key authors like Burris et al. [2000], who studied the maxillary arch sizes and shapes in American whites and blacks, Poggio et al. [2000] who pointed out the deficiencies in using biometrical methods in describing the dental arch curvature, and Noroozi et al. [2001] who showed that the beta function was solely insufficient to describe an expanded square dental arch form, perhaps, constitute some of the most relevant mathematical analyses of recent years.

More recently, one of the most relevant analyses seems to have been carried out by AlHarbi and others [2006] who essentially studied the dental arch curvature of individuals in normal occlusion. They studied 40 sets of plaster dental casts – both upper and lower – of male and female subjects from ages 18 to 25 years. Although their samples were from adults, they considered four most relevant functions, namely, the beta function, the polynomial functions, the natural cubic splines, and the Hermite cubic splines. They found that, whereas the polynomials of 4^th order best fit the dental arch exhibiting symmetrical form, the Hermite cubic splines best described those dental arch curves which were irregular in shape, and were particularly useful in tracking treatment variations. They formed the opinion at the end of their study of subjects – all sourced, incidentally, from nationals of Saudi Arabia – that the 4^th order polynomials could be effectively used to define a smooth dental arch curve which could further be applied into fabricating custom arch wires or a fixed orthodontic apparatus, which could substantially aid in dental arch reconstruction or even in enhancement of esthetic beauty in patients.

Comparison of Different Models for Analysing the Dental Arch

The dental arch has emerged as an important part of modern dentistry for a variety reasons. The need for an early detection and prevention of malocclusion is one important reason whereby dentists hope to ensure a normal and ideal permanent dentition. Dentists also increasingly wish to facilitate normal facial appearance in case of teeth and space abnormalities in children and adults. What constitutes the ideal occlusion, ideal intra-arch and adjacent space and correct arch curvature is a matter of comparison among leading dentists and orthodontists.

Previous studies done in analyzing dental arch shape have used conventional anatomical points on incisal edges and on molar cusp tips so as to classify forms of the dental arch through various mathematical forms like ellipse, parabola, cubical spline, etc, as has been mentioned in the foregoing paragraphs. Other geometric shapes used to describe and measure the dental arch include the catenary curves. Hayashi [1962] used mathematical equations of the form: y = axⁿ + e and applied them to anatomic landmarks on buccal cusps and incisal edges of numerous dental casts. However, the method was complex and required estimation of the parameters like, etc. Also, Hayashi did not consider the asymmetrical curvature of the arch. In contrast, Lu [1966] introduced the concept of fourth degree polynomial for defining the dental arch curve. Later, Biggerstaff [1973] introduced a generalized quadratic equation for studying the close fit of shapes like the parabola, hyperbola and ellipse for describing the form of the human dental arch. However, sixth degree polynomials ensured a better curve fit as mentioned in studies by Pepe [1975]. Many authors like Biggerstaff [1972] have used a parabola of the form x² = -2py for describing the shape of the dental arch while others like Pepe [1975] have stressed on the catenary curve form defined by the equation y = (e^x + e^-x)/2. Biggerstaff [1973] has also mentioned of the equation (x²/b²) + (y²/a²) = 1 that defines an ellipse. BeGole [1980] even developed a computer program in FORTRAN which was used to interpolate a cubic spline for individual subjects who were studied to effectively find out the perfect mathematical model to define the human dental arch. The method due to BeGole essentially utilized the cubic equations and the splines used in analysis were either symmetrical or asymmetrical. Another method, finite element analysis used in comparing dental-arch forms was affected by homology function and the drawbacks of element design. Another multivariate principal component analyses, as performed by Buschang et al. [1994] so as to determine size and shape factors from numerous linear measurements could not satisfactorily explain major variations in dental arch forms and the method failed to provide for a larger generalization in explaining the arch forms.

Analysing Dental Arch Curve in Children in Normal Occlusion

Various studies have been conducted by different experts for defining human dental arch curves by a mathematical model and whose curvature has assumed importance, particularly in prediction, correction and alignment of dental arch in children in normal occlusion. The study of children in primary dentition have led to some notable advances in dental care and treatment of various dental diseases and conditions, although, an exact mathematical model for the dental arch curve is yet to be arrived at. Some characteristic features that have emerged during the course of various studies over time indicate that no single arch form could be found to relate to all types of samples studied since the basic objectives, origin and heredity of the children under study, the drawbacks of the various mathematical tools, etc, do inhibit a satisfactory and perfect fit of any one model in describing the dental arch form to any degree of correction. However, it has been evident through the years of continuous study by dentists and clinical orthodontists that children exhibit certain common features during their childhood, when their dentition is yet to develop into permanent dental form. For example, a common feature is the eruption of primary dentition in children that generally follows a fixed pattern. The time of eruption of various teeth like incisors, molars, canines, etc follow this definite pattern over the growing up years of the child. The differences of teeth forms, shape, size, arch spacing and curvature, etc, that characterize a given sample under study for mathematical analysis, also essentially vary with the nationality and ethnic origin of a child. In one longitudinal study by Henrikson et al. [2001] that studied 30 children of Scandinavian origin with normal occlusion, it was found that when children pass from adolescence into adulthood, a significant lack of stability in arch form was discernible. In another study, experts have also indicated that dental arches in some children were symmetrical, while in others this was not so, indicating that symmetrical form of a dental arch was not a prerequisite for normal occlusion. All these studies, based on mathematical analysis of one kind or another, have thrown up substantial data. But the studies have not been able to achieve a high degree of correlation so as to deliver a generalized theory that can satisfactorily associate a single mathematical model for all dental arch forms in children with normal occlusion.

The various research studies point to different mathematical models as better fit for defining the human dental arch, which fact is perhaps due to the differences in perspectives, research conditions, basic assumptions and varied sample types and sizes used by the various researchers. Thus, while fitting the human dental arch with a mathematical curve, Biggerstaff [1972] chose the quadratic equation as being appropriate in describing the common dental arch forms, viz, parabola, hyperbola and ellipse. However, Lu [1966] chose the 4^th degree polynomial as adequately representing such dental arch curves, while still another researcher Pepe [1975] found the catenary curves inferior as a fit than even the quadratic equations, but also found the 6^th order polynomials a far better fit than the 4^th order polynomials. Nonetheless, she did observe some anomalies in her results and felt that the cubic splines could be considered for further research for defining the human dental arch better. Obviously, later research on cubic splines by BeGole [1980] was influenced by this earlier research due to Pepe [1975]. The research mentioned was thus neither conclusive nor able to perfectly define the shape and size of any and every dental arch.

In her study of cubic splines, BeGole [1980], on the basis of previous research on arch curve definition, stated that, ideally, the arch form could be represented by a curve that had immense flexibility; this would then enable better fit on any dental arch, which, throughout childhood and youth, appeared changing and hence could also be altered by dental intervention methods. She felt that the curve must be able to fit all sizes and shapes of the dental arch and must also include asymmetries unlike the usual geometric forms. According to her, the spline was quite useful because of its symmetry, but also because of its versatility in representing all shapes and sizes of dental arch by means of only a suitable selection of the knot points which were what provided the spline its better fit both with regards to asymmetry and its ability to accommodate diverse arch shapes and sizes. The spline curve, she felt, was actually continuous everywhere and made up of so many data points so that it fits exactly at subsets of points called knots, and which is where smoothing occurs ultimately resulting in a mathematically smooth curve. According to BeGole, the cubic spline, when chosen as a mathematical dental form, also effectively eliminates the limitation of straight lines when fit to the posterior segments of the arch and hence offers various advantages in being used for defining the human dental arch, as compared with other methods. BeGole, Pepe, Biggerstaff, Lu and others have no doubt contributed substantially to research on the dental arch and the defining of the dental arch, but even till the present, no study has been able to conclusively establish the shape of the human dental arch as a universal fit for all type of subjects.

Conclusion

Factors that determine satisfactory diagnosis in orthodontic treatment include teeth spacing and size, the dental arch form and size. Commonly used plaster model analysis is cumbersome, whereas many scanning tools, like laser, destructive and computer tomography scans, structured light, magnetic resonance imaging, and ultrasound techniques, do exist now for accurate 3-D reconstruction of the human anatomy. The plaster orthodontic methods can verily be replaced successfully by 3-D models using computer images for arriving at better accurate results of study. The teeth measurement using computer imaging are accurate, efficient and easy to do and would prove to be very useful in measuring tooth and dental arch sizes and also the phenomenon of dental crowding. Mathematical analysis, though now quite old, can be applied satisfactorily in various issues relating to dentistry and the advances in computer imaging, digitalization and computer analysis through state-of-the-art software programs, do herald a new age in mathematical modelling of the human dental arch which could yet bring in substantial advancement in the field of Orthodontics and Pedodontics. This could in turn usher in an ideal dental care and treatment environment so necessary for countering lack of dental awareness and prevalence of dental diseases and inconsistencies in children across the world.

Bibliography

AlHarbi, S., Alkofide, E.A., AlMadi, A. ‘Mathematical analysis of dental arch curvature in normal occlusion’, Angle Orthod, 2006; 78 (2): 281–287.

Andrews, L.F., ‘The six keys to normal occlusion’, Am J Orthod Dentofacial Orthop, 1972; 62 (3): 296-309.

Angle, E.H., ‘Classification of malocclusion’, Dent Cosmos, 1899; 4: 248-264.

Ash, M.M., Ramfjord, S.P., Occlusion, 3rd edn, Philadelphia: W.B. Saunders Co, 1982.

Battagel, J.M., ‘Individualized catenary curves: their relationship to arch form and perimeter’, Braz J Orthod, 1996; 23: 21–28.

BeGole, E.A., ‘Application of the cubic spline function in the description of dental arch form’, J Dent Res., 1980; 59: 1549–1556.

Biggerstaff, R.H., ‘Three variations in dental arch form estimated by a quadratic equation’, J Dent Res, 1972; 51: 1509.

Brader, A.C., ‘Dental arch form related to intra-oral force: PR = C’, Am J Orthod, 1972; 61: 541–561.

Braun, S., Hnat, W.P., Fender, D.E., Legan, H.L., ‘The form of the dental arch’, Angle Orthod, 1998; 68: 29–36.

Burris, B.G., Harris, F.H., ‘Maxillary arch size and shape in American blacks and whites’, Angle Orthod, 2000; 70: 297–302.

Buschang, P.H., Stroud, J., Alexander, R.G., ‘Differences in dental arch morphology among adult females with untreated Class I and Class II malocclusion’, Eur J Orthod, 1994; 16: 47-52.

Facal-Garcia, M., de Nova-Garcia, J., Suarez-Quintanilla, D., ‘The diastemas in deciduous dentition: the relationship to the tooth size and the dental arches dimensions’ J Clin Paediatr Dent, 2001; 26: 65-69.

Ferrario, V.F., Sforza, C., Miani, Jr A., ‘Statistical evaluation of Monson’s sphere in healthy permanent dentitions in man’ Arch Oral Biol, 1997; 42: 365–369.

Ferrario, V.F., Sforza, C., Colombo, A., Ciusa, V., Serrao, G., ‘3- dimensional inclination of the dental axes in healthy permanent dentitions – a cross-sectional study in normal population’, Angle Orthod, 2001; 71: 257–264.

Ferrario, V.F., Sforza, C., Poggio, C.E., Serrao, G., Colombo, A., ‘Three dimensional dental arch curvatures in human adolescents and adults’, Am J Orthod Dentofacial Orthop, 1999; 115: 401–405.

Harris, E.F., ‘A longitudinal study of arch size and form in untreated adults’, Am J Orthod Dentofacial Orthop, 1997; 111: 419–427.

Hayashi, T., A Mathematical Analysis of the Curve of the Dental Arch, Bulletin, Tokyo Medical Dental University, Tokyo, 1962; 3: 175-218.

Hendrikson, J., Persson, M., Thilander, B., ‘Long term stability of dental arch in normal occlusion from 13 to 31 years of age’ Eur J Orthod, 2001; 23: 51-61.

Houston, W.J.B., Stephens, C.D., Tulley, W.J., A Textbook of Orthodontics, Great Britain: Wright, 1992; pp.1-13.

Jones, M.L., Richmond, S., ‘An assessment of the fit of a parabolic curve to pre- and post-treatment dental arches’, Br J Orthod, 1989; 16: 85-93.

Lu, K.H., ‘An Orthogonal Analysis of the Form, Symmetry and Asymmetry of the Dental Arch’, Arch Oral Biol, 1966; 11: 1057-1069.

McDonald, F., Ireland, A.J., Diagnosis of the Orthodontic Patient, New York: Oxford University Press, 1998.

Noroozi, H., Hosseinzadeh, Nik, T., Saeeda, R., ‘The dental arch form revisited’, Angle Orthod, 2001; 71: 386–389.

Oltramari, P.V.P., Conti, A.C., de Castro, F., Navarro, R. de Lima, de Almeida, M.R., de Almeida Pedrin, R.R., Ferreira, F.P.C., ‘Importance of Occlusion Aspects in the Completion of Orthodontic Treatment’, Braz Dent J, 2007; 18(1), ISSN 0103-6440.

Pepe, S.H., ‘Polynomial and catenary curve fits to human dental arches’, J Dent Res., 1975; 54: 1124–1132.

Poggio, C.E., Mancini, E., Salvato, A., ‘Valutazione degli effetti sulla forma d’arcata della terapia fi ssa e della recidiva mediante la thin plate spline analysis’, Ortognatodonzia Italiana, 2000; 9: 345–350.

Prabhakaran, S., Sriram, C.H., Muthu, M.S., Rao, C.R., Sivakumar, N., ‘Dental arch dimensions in primary dentition of children aged three to five years in Chennai and Hyderabad’, In J Dent Res, Chennai, India, 2006; Retrieved from the World Wide.

Ross, I.F., Occlusion: A concept for the clinician, St. Louis: Mosby Company, 1970.

Roth, R.H. 1981, ‘Functional occlusion for the orthodontist’, J Clin Orthod, 1981; 15: 32-51.

Sampson, P.D., ‘Dental arch shape: a statistical analysis using conic sections’, Am J Orthod, 1981; 79: 535–548.